# 基本牛顿方法
𝐆𝑘𝐝𝑘=−𝐠𝑘
𝛼𝑘=1
# 基本思想
当前点𝐱𝑘处选择𝐝𝑘=−𝐇𝑘𝑔𝑘，其中𝐇𝑘为𝐆𝑘的逆矩阵，但是，使用基本牛顿法的前提是目标函数据还有连续二阶导数
# 特点
当初始点比较接近收敛点时且Hessian正定时，基本牛顿方法具有二次收敛性，且具有二次终止性
# Framework
步1 给出x0属于R，sigma>0，k:=0
步2 若终止准则满足，则输出有关信息，停止迭代
步3 由𝐆𝑘𝐝𝑘=−𝐠𝑘计算𝐝𝑘
步4 𝐱𝑘+1=𝐱𝑘+𝐝𝑘，k:=k+1，转步2
# 阻尼牛顿法
𝐱𝑘+1=𝐱𝑘+𝛼𝐝𝑘
# 基本思想
采用一维线搜索得到𝛼𝑘，有𝛼𝑘=min𝛼𝑓(𝐱𝑘+𝛼𝐝𝑘)。
# 特点
阻尼牛顿法可以克服基本牛顿法的局部收敛性，可以保证对于正定的𝐆𝑘，即使𝐱𝑘离最优点稍远，该方法产生的点列仍然能够收敛至最优点
# 拟牛顿方法（BFGS）
𝐝𝑘=−𝐇𝑘𝑔𝑘,𝛼𝑘=min𝛼𝑓(𝐱𝑘+𝛼𝐝𝑘)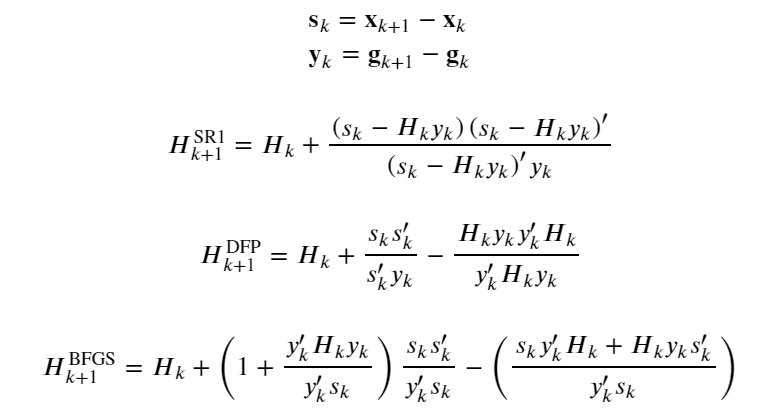 
# 基本思想
构造一个近似矩阵，满足如下条件
（1）只需要𝑓(𝐱)的一阶导数条件
（2）正定，保证下降方向
（3）使得方法具有较快的收敛速度
# 代码实现
首先利用线搜索方法定义一些求最优步长的函数，如黄金区间法。
#首先引入一些必要的包和库
from typing import Callable, Tuple
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import line_search
1
2
3
4
5
6
2
3
4
5
6
def minimize(
f: Callable,
x0: npt.ArrayLike,
grad: Callable,
tol: float = 1e-8,
maxiter: int = 1000
):
x = np.zeros((maxiter+1, x0.shape[0])) # 定义 x 初始存储空间
x[0] = x0
for k in range(maxiter):
d = search_desc_direction(f, x[k], ...) # 确定下降方向
def phi(alpha): return f(x[k] + alpha * d)
alpha = search_step_length(phi, ...) # 确定最优步长
x[k+1] = x[k] + alpha * d
# if np.linalg.norm(g(x[k+1])) <= tol:
# if f(x[k]) - f(x[k+1]) <= tol:
if np.linalg.norm(x[k] - x[k+1]) <= tol:
break
return x[k+1], f(x[k+1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def find_unimodal_interval(
phi: Callable,
alpha0: float,
gamma: float = 0.1,
t: float = 2.0,
max_iter: int = 1000
):
alpha_old = alpha0
phi_alpha_old = phi(alpha_old)
for i in range(max_iter):
alpha = alpha_old + gamma
phi_alpha = phi(alpha)
if phi_alpha >= phi_alpha_old or alpha <= 0:
if i == 0:
gamma = -gamma
alpha_other = alpha
else:
break
else:
gamma = t * gamma
alpha_other = alpha_old
alpha_old = alpha
phi_alpha_old = phi_alpha
return min(alpha_other, alpha), max(alpha_other, alpha)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def minimize_scalar(
phi: Callable,
bounds=None,
method: str = 'brent',
tol: float = None,
options=None
):
pass
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
# 0.618方法
def minimize_scalar_golden(
phi: Callable,
bounds: Tuple[float],
tol: float = 1e-8
):
tau = 0.61803399
a, b = min(bounds), max(bounds)
h = b - a
# Required steps to achieve tolerance
n = int(np.ceil(np.log(tol / h) / np.log(tau)))
a_l, a_r = a + (1 - tau) * h, a + tau * h
phi_l, phi_r = phi(a_l), phi(a_r)
for _ in range(n - 1):
h = tau * h
if phi_l < phi_r:
b, a_r, phi_r = a_r, a_l, phi_l
a_l = a + (1 - tau) * h
phi_l = phi(a_l)
else:
a, a_l, phi_l = a_l, a_r, phi_r
a_r = a + tau * h
phi_r = phi(a_r)
if phi_l < phi_r:
alpha_star = (a + a_r) / 2
else:
alpha_star = (a_l + b) / 2
return alpha_star
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
然后解决具体问题
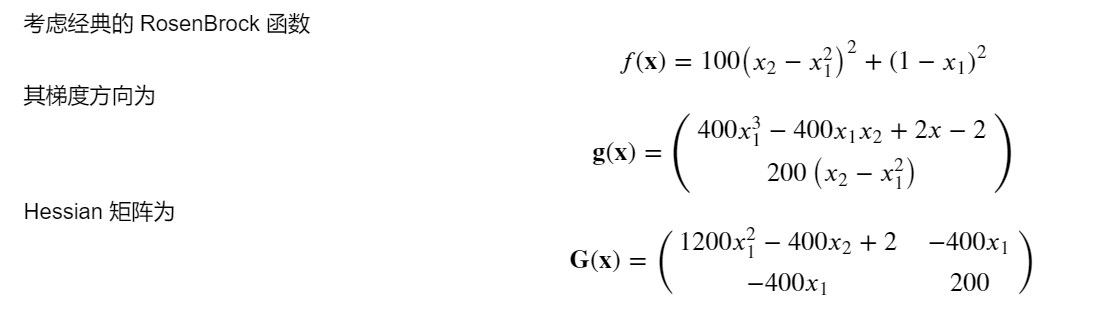
# 给定初始点
x0 = np.array([-1.2, 1])
# 给出函数、梯度与hessian矩阵
def rosenbrock(x):
return 100 * (x[1] - x[0]**2) ** 2 + (1 - x[0]) ** 2
def rosenbrock_grad(x):
return np.array([400*x[0]**3-400*x[0]*x[1]+2*x[0]-2,200*(x[1]-x[0]**2)])
def rosenbrock_hess(x):
return np.array([[1200*x[0]**2-400*x[1]+2, -400*x[0]], [-400*x[0],200]])
x = np.linspace(-2, 2, 250)
# 画出这个函数
def plot_trace(trace):
x = np.linspace(-2, 2, 250)
y = np.linspace(-2, 4, 250)
X, Y = np.meshgrid(x, y)
Z = rosenbrock([X, Y])
trace, y_trace = trace[:, 0], trace[:, 1]
z_trace = rosenbrock((trace, y_trace))
fig = plt.figure(figsize=(16, 8))
ax = fig.add_subplot(1, 2, 1, projection="3d")
ax.plot_surface(X, Y, Z, cmap="jet", alpha=.4, edgecolor='none')
ax.plot(trace, y_trace, z_trace, color='r', marker='*', alpha=.4)
anglesx = trace[1:] - trace[:-1]
anglesy = y_trace[1:] - y_trace[:-1]
ax = fig.add_subplot(1, 2, 2)
ax.contour(X, Y, Z, 50, cmap="jet")
ax.scatter(trace, y_trace, color='r', marker='*')
ax.quiver(trace[:-1], y_trace[:-1], anglesx, anglesy,
scale_units='xy', angles='xy', scale=1, color='r', alpha=.3)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
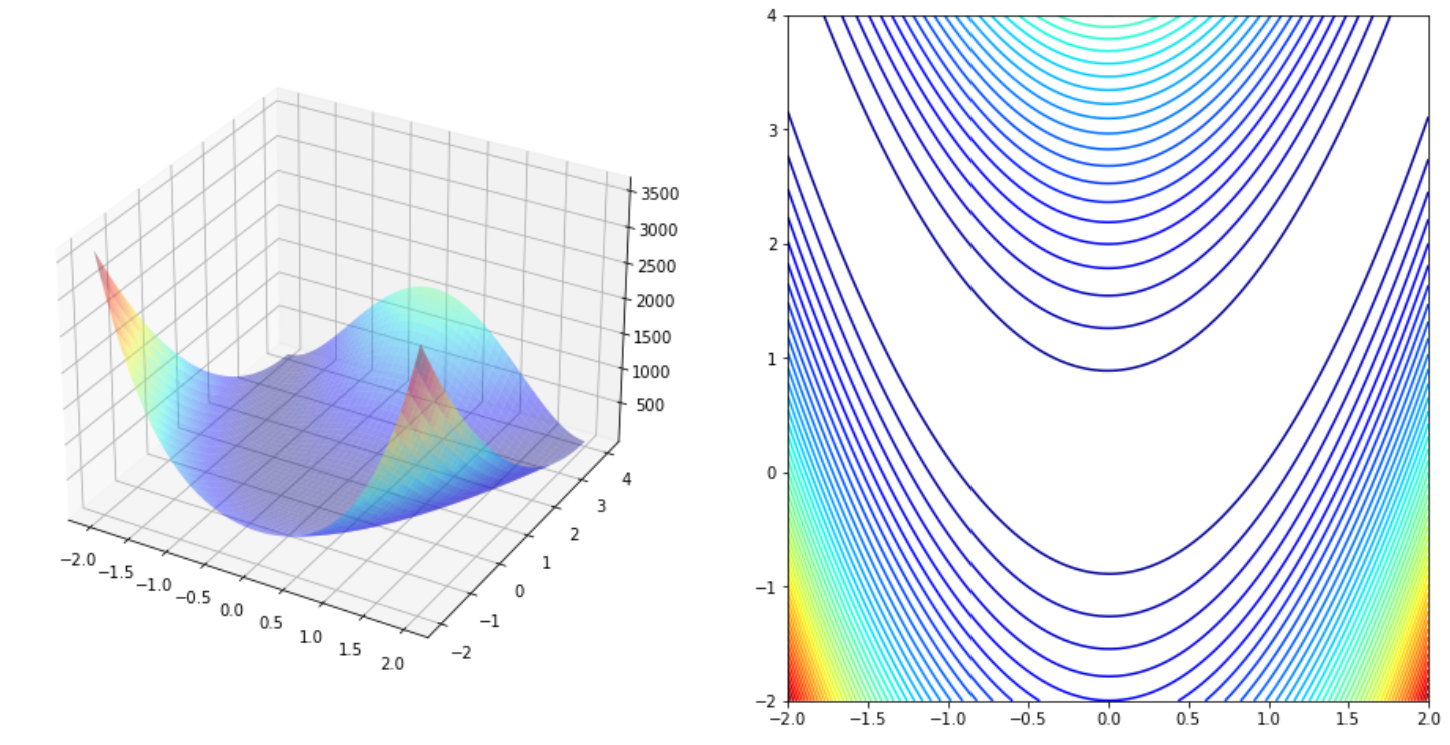
# 基本牛顿法
def minimize_newton(
f,
x0,
grad,
hess,
maxiter=1000,
tol=1e-8
):
x = x0
fval_prev = f(x)
trace = np.empty((maxiter+1, len(x0)))
trace[0] = x0
for k in range(maxiter):
G = hess(x)
g = grad(x)
d = - np.linalg.inv(G) @ g
x = x + d
trace[k+1] = x
fval = f(x)
print(x, fval)
# if fval_prev - fval < tol:
if np.linalg.norm(g) < tol:
break
fval_prev = fval
return x, fval, trace[:k+1,:]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
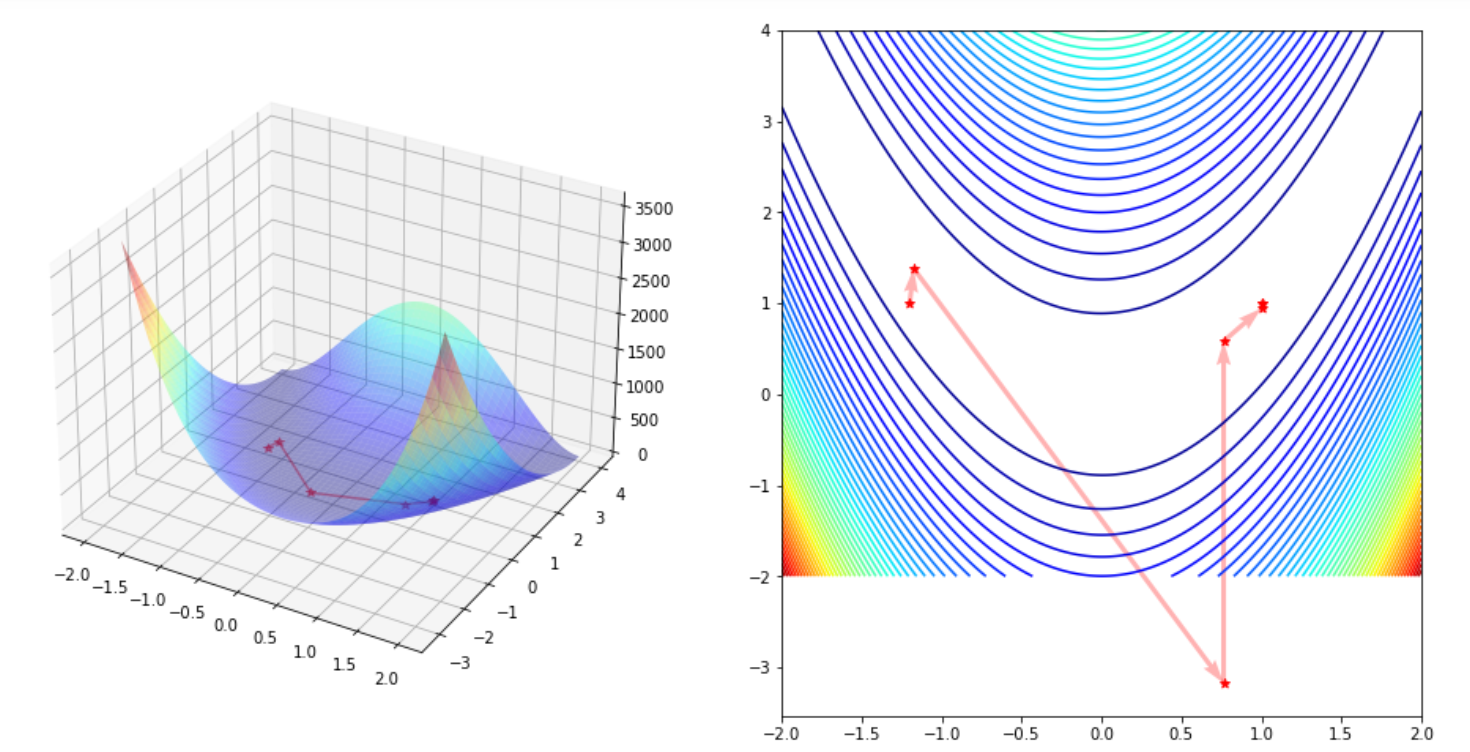
#阻尼牛顿法
def minimize_newton_damp(
f,
x0,
grad,
hess,
maxiter=1000,
tol=1e-8
):
x = x0
fval_prev = f(x)
trace = np.empty((maxiter+1, len(x0)))
trace[0] = x0
for k in range(maxiter):
G = hess(x)
g = grad(x)
d = - np.linalg.inv(G) @ g
# alpha, _, _, _, _, _ = line_search(f, grad, x, d)
def phi(alpha): return f(x+alpha*d)
bounds = find_unimodal_interval(phi, 0)
alpha = minimize_scalar_golden(phi, bounds)
x = x + alpha * d
trace[k+1] = x
fval = f(x)
print(x, fval)
if fval_prev - fval < tol:
# if np.linalg.norm(g) < tol:
break
fval_prev = fval
return x, fval, trace[:k+1,:]
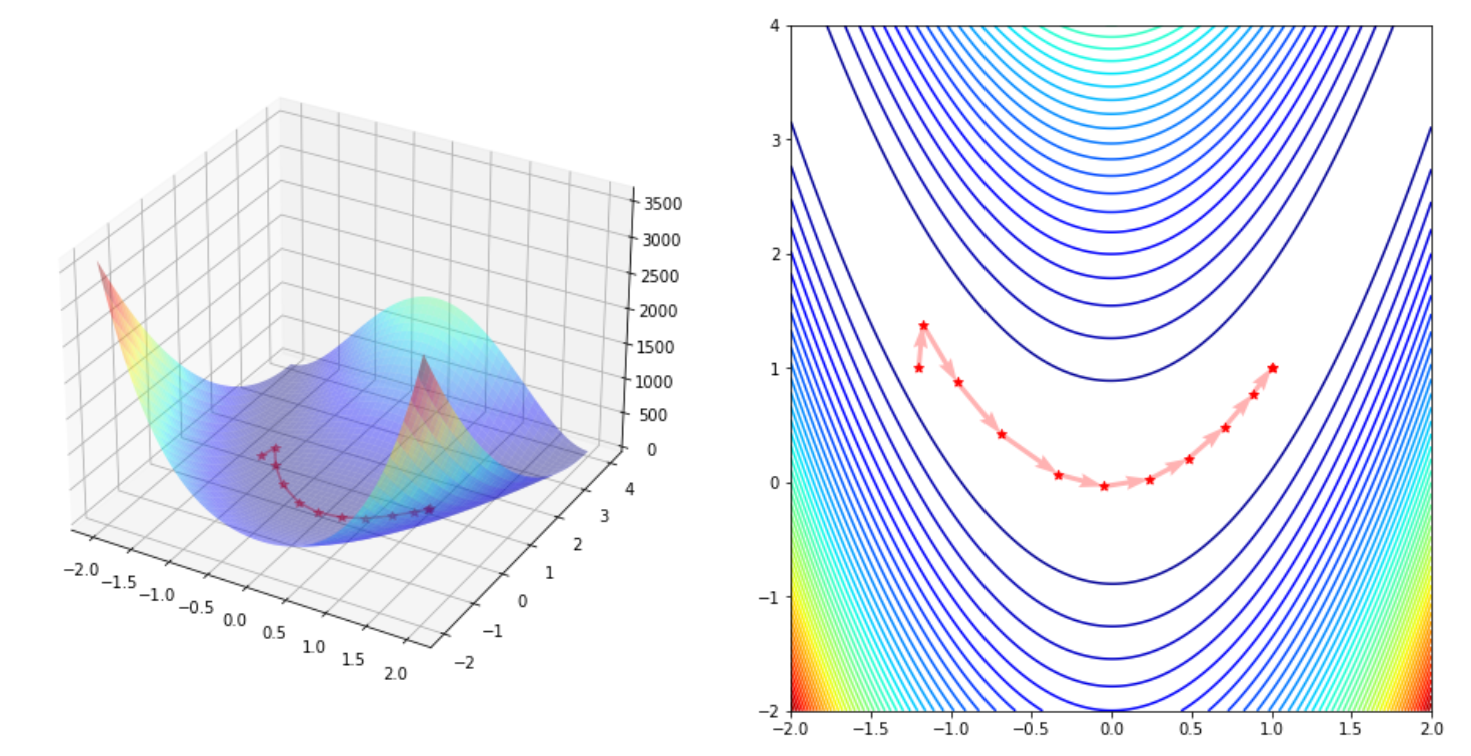
x, fval, trace = minimize_newton_damp(rosenbrock, x0, rosenbrock_grad, rosenbrock_hess)
print("Optimal Point: (%.4f, %.4f), Optimal Value %.4f" % (x[0], x[1], fval))
plot_trace(trace)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#拟牛顿方法之BFGS方法
def minimize_quasi_newton_bfgs(
f,
x0,
grad,
maxiter=1000,
tol=1e-8
):
x, fval_prev = x0, f(x0)
H = np.eye(len(x0))
g = grad(x0)
trace = np.empty((maxiter+1,len(x0)))
trace[0] = x0
for k in range(maxiter):
d = - H @ g
alpha, _, _, _, _, _ = line_search(f, grad, x, d)
# def phi(alpha): return f(x+alpha*d)
# bounds = find_unimodal_interval(phi, 0)
# alpha = minimize_scalar_golden(phi, bounds)
x_new = x + alpha * d
g_new = grad(x_new)
s = x_new - x
y = g_new - g
s = s[:,np.newaxis]
y = y[:,np.newaxis]
delta_H = (1 + (y.T @ H @ y) / (y.T @ s)) * ((s @ s.T) / (y.T @ s)) - ((s @ y.T @ H + H @ y @ s.T) / (y.T @ s))
H = H + delta_H
x, g = x_new, g_new
trace[k+1] = x
fval = f(x)
print(x, fval)
if fval_prev - fval < tol:
# if np.linalg.norm(g) < tol:
break
fval_prev = fval
return x, fval, trace[:k+1,:]
%%time
x, fval, trace = minimize_quasi_newton_bfgs(rosenbrock, x0, rosenbrock_grad)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 
layout: post title: 无约束优化问题中的牛顿型方法 date: 2021-11-20 author: LZY categories:
- 数据分析部 tags:
- 牛顿型方法
# 基本牛顿方法
𝐆𝑘𝐝𝑘=−𝐠𝑘
𝛼𝑘=1
# 基本思想
当前点𝐱𝑘处选择𝐝𝑘=−𝐇𝑘𝑔𝑘，其中𝐇𝑘为𝐆𝑘的逆矩阵，但是，使用基本牛顿法的前提是目标函数据还有连续二阶导数
# 特点
当初始点比较接近收敛点时且Hessian正定时，基本牛顿方法具有二次收敛性，且具有二次终止性
# Framework
步1 给出x0属于R，sigma>0，k:=0
步2 若终止准则满足，则输出有关信息，停止迭代
步3 由𝐆𝑘𝐝𝑘=−𝐠𝑘计算𝐝𝑘
步4 𝐱𝑘+1=𝐱𝑘+𝐝𝑘，k:=k+1，转步2
# 阻尼牛顿法
𝐱𝑘+1=𝐱𝑘+𝛼𝐝𝑘
# 基本思想
采用一维线搜索得到𝛼𝑘，有𝛼𝑘=min𝛼𝑓(𝐱𝑘+𝛼𝐝𝑘)。
# 特点
阻尼牛顿法可以克服基本牛顿法的局部收敛性，可以保证对于正定的𝐆𝑘，即使𝐱𝑘离最优点稍远，该方法产生的点列仍然能够收敛至最优点
# 拟牛顿方法（BFGS）
𝐝𝑘=−𝐇𝑘𝑔𝑘,𝛼𝑘=min𝛼𝑓(𝐱𝑘+𝛼𝐝𝑘)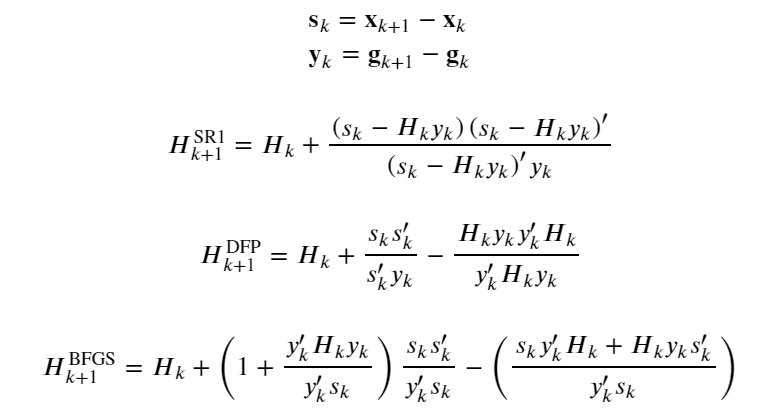
# 基本思想
构造一个近似矩阵，满足如下条件
（1）只需要𝑓(𝐱)的一阶导数条件
（2）正定，保证下降方向
（3）使得方法具有较快的收敛速度
# 代码实现
首先利用线搜索方法定义一些求最优步长的函数，如黄金区间法。
#首先引入一些必要的包和库
from typing import Callable, Tuple
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import line_search
1
2
3
4
5
6
2
3
4
5
6
def minimize(
f: Callable,
x0: npt.ArrayLike,
grad: Callable,
tol: float = 1e-8,
maxiter: int = 1000
):
x = np.zeros((maxiter+1, x0.shape[0])) # 定义 x 初始存储空间
x[0] = x0
for k in range(maxiter):
d = search_desc_direction(f, x[k], ...) # 确定下降方向
def phi(alpha): return f(x[k] + alpha * d)
alpha = search_step_length(phi, ...) # 确定最优步长
x[k+1] = x[k] + alpha * d
# if np.linalg.norm(g(x[k+1])) <= tol:
# if f(x[k]) - f(x[k+1]) <= tol:
if np.linalg.norm(x[k] - x[k+1]) <= tol:
break
return x[k+1], f(x[k+1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def find_unimodal_interval(
phi: Callable,
alpha0: float,
gamma: float = 0.1,
t: float = 2.0,
max_iter: int = 1000
):
alpha_old = alpha0
phi_alpha_old = phi(alpha_old)
for i in range(max_iter):
alpha = alpha_old + gamma
phi_alpha = phi(alpha)
if phi_alpha >= phi_alpha_old or alpha <= 0:
if i == 0:
gamma = -gamma
alpha_other = alpha
else:
break
else:
gamma = t * gamma
alpha_other = alpha_old
alpha_old = alpha
phi_alpha_old = phi_alpha
return min(alpha_other, alpha), max(alpha_other, alpha)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def minimize_scalar(
phi: Callable,
bounds=None,
method: str = 'brent',
tol: float = None,
options=None
):
pass
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
# 0.618方法
def minimize_scalar_golden(
phi: Callable,
bounds: Tuple[float],
tol: float = 1e-8
):
tau = 0.61803399
a, b = min(bounds), max(bounds)
h = b - a
# Required steps to achieve tolerance
n = int(np.ceil(np.log(tol / h) / np.log(tau)))
a_l, a_r = a + (1 - tau) * h, a + tau * h
phi_l, phi_r = phi(a_l), phi(a_r)
for _ in range(n - 1):
h = tau * h
if phi_l < phi_r:
b, a_r, phi_r = a_r, a_l, phi_l
a_l = a + (1 - tau) * h
phi_l = phi(a_l)
else:
a, a_l, phi_l = a_l, a_r, phi_r
a_r = a + tau * h
phi_r = phi(a_r)
if phi_l < phi_r:
alpha_star = (a + a_r) / 2
else:
alpha_star = (a_l + b) / 2
return alpha_star
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
然后解决具体问题
# 给定初始点
x0 = np.array([-1.2, 1])
# 给出函数、梯度与hessian矩阵
def rosenbrock(x):
return 100 * (x[1] - x[0]**2) ** 2 + (1 - x[0]) ** 2
def rosenbrock_grad(x):
return np.array([400*x[0]**3-400*x[0]*x[1]+2*x[0]-2,200*(x[1]-x[0]**2)])
def rosenbrock_hess(x):
return np.array([[1200*x[0]**2-400*x[1]+2, -400*x[0]], [-400*x[0],200]])
x = np.linspace(-2, 2, 250)
# 画出这个函数
def plot_trace(trace):
x = np.linspace(-2, 2, 250)
y = np.linspace(-2, 4, 250)
X, Y = np.meshgrid(x, y)
Z = rosenbrock([X, Y])
trace, y_trace = trace[:, 0], trace[:, 1]
z_trace = rosenbrock((trace, y_trace))
fig = plt.figure(figsize=(16, 8))
ax = fig.add_subplot(1, 2, 1, projection="3d")
ax.plot_surface(X, Y, Z, cmap="jet", alpha=.4, edgecolor='none')
ax.plot(trace, y_trace, z_trace, color='r', marker='*', alpha=.4)
anglesx = trace[1:] - trace[:-1]
anglesy = y_trace[1:] - y_trace[:-1]
ax = fig.add_subplot(1, 2, 2)
ax.contour(X, Y, Z, 50, cmap="jet")
ax.scatter(trace, y_trace, color='r', marker='*')
ax.quiver(trace[:-1], y_trace[:-1], anglesx, anglesy,
scale_units='xy', angles='xy', scale=1, color='r', alpha=.3)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 基本牛顿法
def minimize_newton(
f,
x0,
grad,
hess,
maxiter=1000,
tol=1e-8
):
x = x0
fval_prev = f(x)
trace = np.empty((maxiter+1, len(x0)))
trace[0] = x0
for k in range(maxiter):
G = hess(x)
g = grad(x)
d = - np.linalg.inv(G) @ g
x = x + d
trace[k+1] = x
fval = f(x)
print(x, fval)
# if fval_prev - fval < tol:
if np.linalg.norm(g) < tol:
break
fval_prev = fval
return x, fval, trace[:k+1,:]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#阻尼牛顿法
def minimize_newton_damp(
f,
x0,
grad,
hess,
maxiter=1000,
tol=1e-8
):
x = x0
fval_prev = f(x)
trace = np.empty((maxiter+1, len(x0)))
trace[0] = x0
for k in range(maxiter):
G = hess(x)
g = grad(x)
d = - np.linalg.inv(G) @ g
# alpha, _, _, _, _, _ = line_search(f, grad, x, d)
def phi(alpha): return f(x+alpha*d)
bounds = find_unimodal_interval(phi, 0)
alpha = minimize_scalar_golden(phi, bounds)
x = x + alpha * d
trace[k+1] = x
fval = f(x)
print(x, fval)
if fval_prev - fval < tol:
# if np.linalg.norm(g) < tol:
break
fval_prev = fval
return x, fval, trace[:k+1,:]
x, fval, trace = minimize_newton_damp(rosenbrock, x0, rosenbrock_grad, rosenbrock_hess)
print("Optimal Point: (%.4f, %.4f), Optimal Value %.4f" % (x[0], x[1], fval))
plot_trace(trace)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#拟牛顿方法之BFGS方法
def minimize_quasi_newton_bfgs(
f,
x0,
grad,
maxiter=1000,
tol=1e-8
):
x, fval_prev = x0, f(x0)
H = np.eye(len(x0))
g = grad(x0)
trace = np.empty((maxiter+1,len(x0)))
trace[0] = x0
for k in range(maxiter):
d = - H @ g
alpha, _, _, _, _, _ = line_search(f, grad, x, d)
# def phi(alpha): return f(x+alpha*d)
# bounds = find_unimodal_interval(phi, 0)
# alpha = minimize_scalar_golden(phi, bounds)
x_new = x + alpha * d
g_new = grad(x_new)
s = x_new - x
y = g_new - g
s = s[:,np.newaxis]
y = y[:,np.newaxis]
delta_H = (1 + (y.T @ H @ y) / (y.T @ s)) * ((s @ s.T) / (y.T @ s)) - ((s @ y.T @ H + H @ y @ s.T) / (y.T @ s))
H = H + delta_H
x, g = x_new, g_new
trace[k+1] = x
fval = f(x)
print(x, fval)
if fval_prev - fval < tol:
# if np.linalg.norm(g) < tol:
break
fval_prev = fval
return x, fval, trace[:k+1,:]
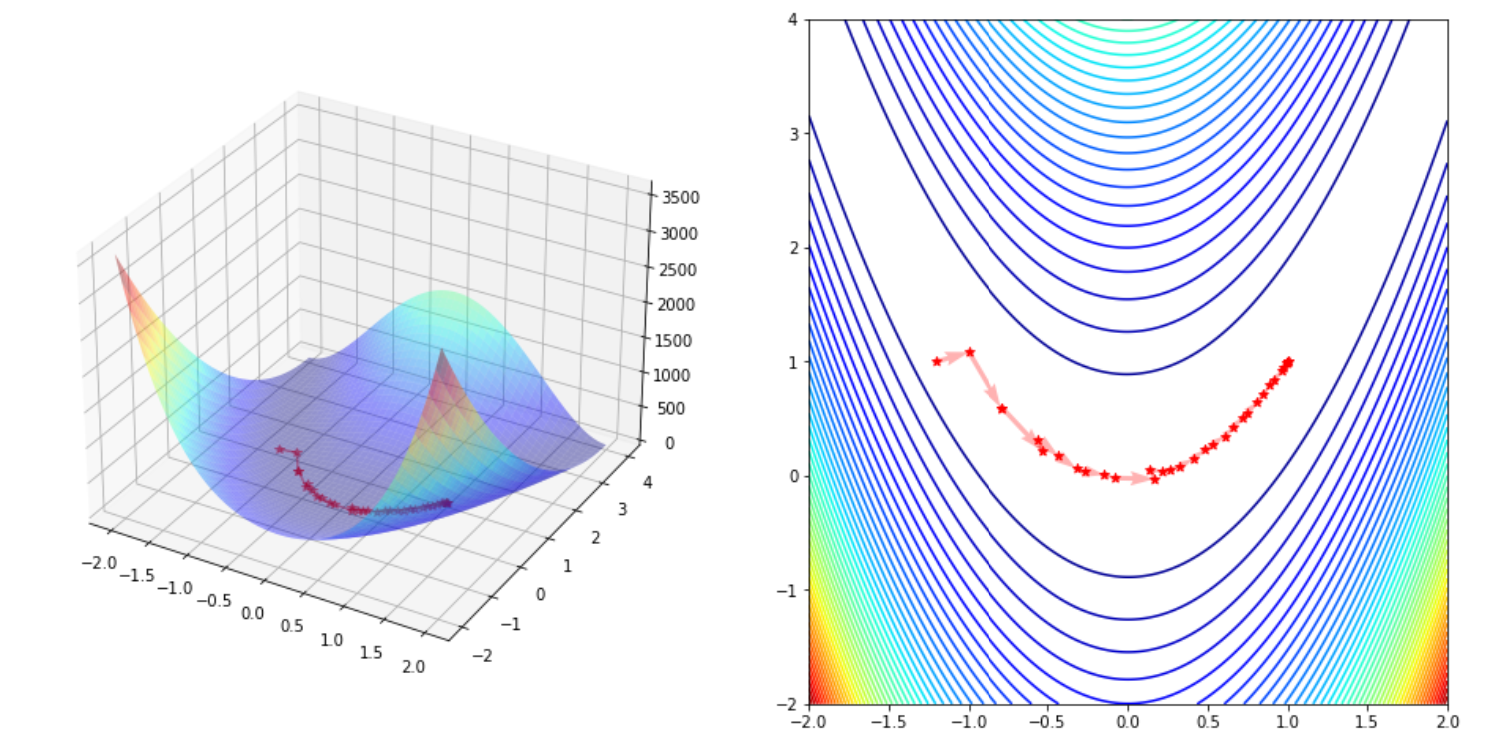
%%time
x, fval, trace = minimize_quasi_newton_bfgs(rosenbrock, x0, rosenbrock_grad)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
