我们将开始一个专题, 从数据收集, 数据整理, 到建模分析, 结果展示共四个部分, 系统地学习数据分析. (这里我先写**(二)数据整理部分**)
# 探索性数据分析简述
探索性数据分析 (Exploratory Data Analysis, 简称 EDA), 是指对已有的数据, 通过作图, 制表, 方程拟合等手段探索数据的结构和规律的一种方法.
EDA 是数据分析中不可或缺的一个步骤, 也是得到原始数据后第一件需要做的事情. 通过 EDA, 研究者能对原始数据的结构, 质量, 规律有一个大致的了解, 从而得到启发, 更好地进行后续的建模与分析.
# 步骤
# 1. 检查数据总体情况
# 加载所需要的库
import numpy as np
import pandas as pd
# 加载数据
df = pd.read_csv('titanic/train.csv')
df.head(10) # 看看是否加载正确
2
3
4
5
6
7
df.describe()
PassengerId Survived Pclass Age SibSp \
count 891.000000 891.000000 891.000000 714.000000 891.000000
mean 446.000000 0.383838 2.308642 29.699118 0.523008
std 257.353842 0.486592 0.836071 14.526497 1.102743
min 1.000000 0.000000 1.000000 0.420000 0.000000
25% 223.500000 0.000000 2.000000 20.125000 0.000000
50% 446.000000 0.000000 3.000000 28.000000 0.000000
75% 668.500000 1.000000 3.000000 38.000000 1.000000
max 891.000000 1.000000 3.000000 80.000000 8.000000
Parch Fare
count 891.000000 891.000000
mean 0.381594 32.204208
std 0.806057 49.693429
min 0.000000 0.000000
25% 0.000000 7.910400
50% 0.000000 14.454200
75% 0.000000 31.000000
max 6.000000 512.329200
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 1.1 缺失值检查与处理
# 方法一
df.info()
# 输出如下, 可以看到, 一共有891个entry(条目), 除了Age, Cabin, Embarked属性, 其他都不含空值
2
3
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 891 non-null int64
1 Survived 891 non-null int64
2 Pclass 891 non-null int64
3 Name 891 non-null object
4 Sex 891 non-null object
5 Age 714 non-null float64
6 SibSp 891 non-null int64
7 Parch 891 non-null int64
8 Ticket 891 non-null object
9 Fare 891 non-null float64
10 Cabin 204 non-null object
11 Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 方法二, 由于该输出容易看眼花, 不推荐
df.isnull()
# 但是在后面加上.sum()后效果更好
# df.isnull().sum()
2
3
4
5
# 方法三, 具体查看缺失某一属性的条目
df[df.Age.isnull()]
# df[df.Age.isnull()].index
2
3
4
# 缺失数据的类型:
- 随机丢失: 出于样本其他属性原因而丢失. 例如性别为"女性"的样本"年龄"属性有更高概率的缺失
- 完全随机丢失: 数据的丢失是完全随机的. 例如一张表的某一部分被一水渍污染而模糊不清
- 非随机丢失: 出于该属性自身原因而丢失. 例如高收入人群不愿透露自身收入
# 缺失值的影响:
- 使系统丢失有用的信息
- 包含空值的数据可能影响后续的建模过程, 使模型偏倚
# 缺失值的处理:
删除法:
DataFrame.dropna()-官方文档删除条目(样本)
df_dropped_1 = df.dropna(inplace=False) # dropna()会drop掉df中任何含有空值属性的条目,直接使条目数骤降,并且注意是否启用inplace参数 df_dropped_1.info() # 可以从输出中看到, 条目数由891下降到了183, 故如果数据中缺失值较多, 应进行更加细致的删除 # 例如控制指定属性类别缺失时drop, 或每一条目的空值个数达到指定个数时drop # 详细用法见官方文档链接1
2
3
4
5
6
7<class 'pandas.core.frame.DataFrame'> Int64Index: 183 entries, 1 to 889 Data columns (total 12 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 PassengerId 183 non-null int64 1 Survived 183 non-null int64 2 Pclass 183 non-null int64 3 Name 183 non-null object 4 Sex 183 non-null object 5 Age 183 non-null float64 6 SibSp 183 non-null int64 7 Parch 183 non-null int64 8 Ticket 183 non-null object 9 Fare 183 non-null float64 10 Cabin 183 non-null object 11 Embarked 183 non-null object dtypes: float64(2), int64(5), object(5) memory usage: 18.6+ KB1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
删除属性(特征)
df_dropped_2 = df.dropna(axis='columns', inplace=False) df_dropped_2.info() # 可以看到, 特征种类数从12降到了9个, 而条目数仍为8911
2
3<class 'pandas.core.frame.DataFrame'> RangeIndex: 891 entries, 0 to 890 Data columns (total 9 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 PassengerId 891 non-null int64 1 Survived 891 non-null int64 2 Pclass 891 non-null int64 3 Name 891 non-null object 4 Sex 891 non-null object 5 SibSp 891 non-null int64 6 Parch 891 non-null int64 7 Ticket 891 non-null object 8 Fare 891 non-null float64 dtypes: float64(1), int64(5), object(3) memory usage: 62.8+ KB1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16# 观察下 Cabin 属性 pd.set_option('display.max_rows', None) # 让pandas完全展示数据 print(df.Cabin.describe()) df.Cabin.value_counts() # 可以发现, Cabin属性数据缺失过于严重, 且过于分散, 故我们可以用df.drop('Cabin',axis=1)暂时删掉这一列.1
2
3
4
5count 204 unique 147 top G6 freq 4 Name: Cabin, dtype: object G6 4 B96 B98 4 C23 C25 C27 4 E101 3 C22 C26 3 F2 3 D 3 F33 3 E24 2 F G73 2 C65 2 B49 2 ... A16 1 B3 1 E58 1 T 1 C148 1 A36 1 C110 1 D6 1 A10 1 B4 11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29其实, 探索 Cabin 特征会有奇妙的发现, 但这属于后面的内容, 探索代码如下
data_train['CabinCat'] = data_train['Cabin'].copy() data_train.loc[ (data_train.CabinCat.notnull()), 'CabinCat' ] = "No" data_train.loc[ (data_train.CabinCat.isnull()), 'CabinCat' ] = "Yes" fig, ax = plt.subplots(figsize=(10,5)) sns.countplot(x='CabinCat', hue='Survived',data=data_train) plt.show()1
2
3
4
5
6
7
插补法
平均值, 众数
# 使用平均数填充 df['Age'].fillna(df['Age'].mean(), inplace=True) df['Age'].count() # >>891 # 众数填充:将.mean()改为.mode()即可1
2
3
4
5
6
7热卡填充(就近补齐), 略
K 近邻均值
KNNImputer-官方文档# 利用'SibSp','Parch'特征来预测 Age 特征, 至于为什么用这两个属性, 见后文 from sklearn.impute import KNNImputer imputer = KNNImputer(n_neighbors=5) df[['SibSp','Parch','Age']] = imputer.fit_transform(df[['SibSp','Parch','Age']])1
2
3
4# 更高级的方法, 训练多个预测模型, 其中使用不同的K值估算缺失值, 并查看哪个模型表现最佳 # 选择"随机森林"算法进行训练, RMSE 用于验证 # 使用当前的K值执行插补 # 将数据集分为训练和测试子集 # 拟合随机森林模型 # 预测测试集 # 使用RMSE进行评估 from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestRegressor from sklearn.metrics import mean_squared_error rmse = lambda y, yhat: np.sqrt(mean_squared_error(y, yhat)) def optimize_k(data, target): errors = [] for k in range(1, 20, 2): imputer = KNNImputer(n_neighbors=k) imputed = imputer.fit_transform(data[['SibSp','Parch','Age']]) df_imputed = pd.DataFrame(imputed, columns=['SibSp','Parch','Age']) X = df_imputed.drop(target, axis=1) y = df_imputed[target] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) model = RandomForestRegressor() model.fit(X_train, y_train) preds = model.predict(X_test) error = rmse(y_test, preds) errors.append({'K': k, 'RMSE': error}) return errors optimize_k(df, "Age") # 输出如下, 当k=15时误差最小1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34[{'K': 1, 'RMSE': 12.896725109304743}, {'K': 3, 'RMSE': 12.678965119534436}, {'K': 5, 'RMSE': 12.578639271225404}, {'K': 7, 'RMSE': 12.510222355713427}, {'K': 9, 'RMSE': 12.513595889367565}, {'K': 11, 'RMSE': 12.656939408309634}, {'K': 13, 'RMSE': 12.507041631375014}, {'K': 15, 'RMSE': 12.458167450009855}, {'K': 17, 'RMSE': 12.475283664175599}, {'K': 19, 'RMSE': 12.49010794736692}, {'K': 21, 'RMSE': 12.460959655109617}, {'K': 23, 'RMSE': 12.516988087316093}, {'K': 25, 'RMSE': 12.55008353910895}, {'K': 27, 'RMSE': 12.50969152256041}, {'K': 29, 'RMSE': 12.472538055781568}]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
逻辑回归(离散), 线性回归(连续)
LogisticRegression-官方文档LinearRegression-官方文档# 逻辑回归, 数据非Titanic例 from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42) LR = LogisticRegression(C=1.0, penalty='l1', tol=0.01) LR.fit(X_train,y_train) LR.predict(X_test) LR.score(X_test,y_test)1
2
3
4
5
6
7
8
9
10# 线性回归, 数据非Titanic例 from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42) linreg = LinearRegression() linreg.fit(X_train, y_train) y_pred = linreg.predict(X_test) linreg.score(X_test,y_test)1
2
3
4
5
6
7
8
9
10-
# 启用sklearn的试验功能:IterativeImputer from sklearn.experimental import enable_iterative_imputer from sklearn.impute import IterativeImputer imp = IterativeImputer(max_iter=10, random_state=0) imp.fit([[1, 2], [3, 6], [4, 8], [np.nan, 3], [7, np.nan]]) X_test = [[np.nan, 2], [6, np.nan], [np.nan, 6]] print(np.round(imp.transform(X_test)))1
2
3
4
5
6
7 随机样本插补, 略
-
from sklearn.ensemble import RandomForestRegressor def set_missing_ages(df): # 把已有的数值型特征取出来丢进Random Forest Regressor中 age_df = df[['Age','Fare', 'Parch', 'SibSp', 'Pclass']] # 乘客分成已知年龄和未知年龄两部分 known_age = age_df[age_df.Age.notnull()].as_matrix() unknown_age = age_df[age_df.Age.isnull()].as_matrix() # y即目标年龄 y = known_age[:, 0] # X即特征属性值 X = known_age[:, 1:] # fit到RandomForestRegressor之中 rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1) rfr.fit(X, y) # 用得到的模型进行未知年龄结果预测 predictedAges = rfr.predict(unknown_age[:, 1:]) # print predictedAges # 用得到的预测结果填补原缺失数据 df.loc[ (df.Age.isnull()), 'Age' ] = predictedAges return df, rfr1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
不处理
- 贝叶斯网络
- 人工神经网络
# 1.2 异常值检查与处理
一方面, 在构建模型的过程中, 如果算法对异常点敏感, 那么生成的模型并不能对整体样本有一个较好的表达, 从而预测也会不准确. 另一方面, 在某些场景, 异常点带来的信息非常特殊和有用(假异常).
# 检测方法
统计描述法
df.describe() # 可以看到数据的最大值最小值, 比如年龄Age最大为80,最小为0.42,属于正常范围1
2PassengerId Survived Pclass Age SibSp \ count 891.000000 891.000000 891.000000 714.000000 891.000000 mean 446.000000 0.383838 2.308642 29.699118 0.523008 std 257.353842 0.486592 0.836071 14.526497 1.102743 min 1.000000 0.000000 1.000000 0.420000 0.000000 25% 223.500000 0.000000 2.000000 20.125000 0.000000 50% 446.000000 0.000000 3.000000 28.000000 0.000000 75% 668.500000 1.000000 3.000000 38.000000 1.000000 max 891.000000 1.000000 3.000000 80.000000 8.000000 Parch Fare count 891.000000 891.000000 mean 0.381594 32.204208 std 0.806057 49.693429 min 0.000000 0.000000 25% 0.000000 7.910400 50% 0.000000 14.454200 75% 0.000000 31.000000 max 6.000000 512.3292001
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19散点图法
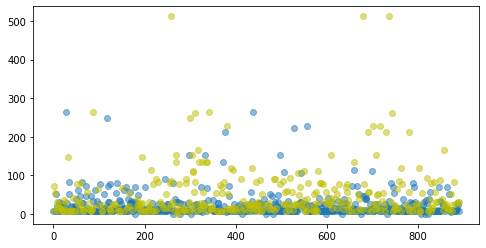
plt.figure(figsize=(10, 6)) # 设置画布大小 ind_0 = df[df['Survived']==0].index # 没有存活的人员索引 ind_1 = df[df['Survived']==1].index plt.scatter(ind_0,df.iloc[ind_0]['Fare'],alpha=0.5,c='b' ) # 未存活的点为蓝色 plt.scatter(ind_1,df.iloc[ind_1]['Fare'],alpha=0.5,c='y' ) # 存活的点为黄色 plt.show() # 可以看到, 有三个点的票价异常高, 可以考虑作为异常点处理1
2
3
4
5
6
7
8
9
10
11
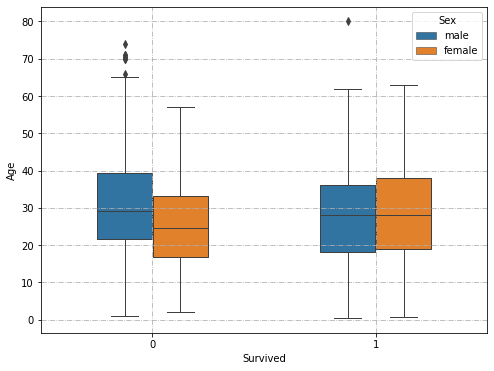
箱线图法
# pandas有自己的箱线图方法: DF.boxplot() # pyplot也有箱线图方法: plt.boxplot() # 推荐使用seaborn的sns.boxplot()方法: import seaborn as sns plt.figure(figsize=(10, 6)) sns.boxplot(x="Survived", y="Age",hue='Sex', data=df, width=0.5, linewidth=1.0) plt.grid(True, linestyle = "-.") # 设置网格线 plt.show()1
2
3
4
5
6
7
8
9
10
11
# 异常值处理方法:
删除含有异常值的样本
ind = df[df['Fare']>400].index # 票价大于400的索引 df.drop(ind,inplace=True) df = df.reindex(index=range(len(df))) # 去掉异常值后重新制定索引1
2
3将其视为缺失值, 再进行缺失值插补
ind = df[df['Fare']>400].index df.iloc[ind] = np.nan1
2不处理
# 1.3 重复值检测
在逻辑回归分析中, 重复数据会影响模型的拟合优度, 影响预测内容准确性. 处理重复值数据有着重要的意义和作用.
首先要分清重复样本的产生原因, 是巧合还是错误. 例如两条身份信息 {'sex': 'male','age': 40,'city': 'Chengdu'} 和 {'sex': 'male','age': 40,'city': 'Chengdu'} 则可能是正好两个不同的人都是来自成都的 40 岁男性, 这就是巧合. 而{'bill_ID': 10001, 'commodity': 'cola', 'amounts': 40}则不可能与其他样本重复, 因为账单编号 bill_ID 和身份证号一样是唯一的.
# 重复值的查看:
df[df.duplicated()]
# 重复值的处理
drop_duplicates -官方文档
df.drop_duplicates(inplace=True) # 去掉重复样本, 仅保留一个
# 1.4 变量编码转换
在后面进行建模的过程中, 算法通常只能处理数值型的数据, 因此需要把例如 male 和 famale 等特征值转换为数值型.
离散变量的编码分两种情况:
- 离散变量是有序的, 即存在大小关系, 如尺码 ['S', 'M', 'L']
- 离散变量是无序的, 即不存在大小关系, 如颜色 ['green', 'red', 'yellow', 'pink']
# 转换方法
使用
DataFrame.replace()方法 -官方文档# 简单易用 df['Sex'].replace({'male':0, 'female':1},inplace=True) df.head() # df.map()方法类似1
2
3
4使用
pandas.get_dummies()方法 -官方文档# pandas.get_dummies() 是一种one-hot编码, 即得到稀疏矩阵 df = df.join(pd.get_dummies(df.Sex)) # 添加新得到的特征: female 和 male 列 df.drop('Sex',axis=1) # 去掉原特征1
2
3使用
sklearn.preprocessing的LabelEncoder-官方文档# 非one-hot编码 from sklearn.preprocessing import LabelEncoder lbl = LabelEncoder() label_dict = dict(zip(df['Sex'].unique(), range(df['Sex'].nunique()))) # df['Sex' + "_labelEncode"] = df['Sex'].map(label_dict) # 此为map()方法 df['Sex' + "_labelEncode"] = lbl.fit_transform(df['Sex'].astype(str)) df.head()1
2
3
4
5
6
7
8
9
10使用
sklearn.preprocessing的OneHotEncoder-官方文档# 当属性取值较多时可以采取本方法 from sklearn.preprocessing import OneHotEncoder ohe = OneHotEncoder(sparse=False) # 设定忽略缺失值见下,或者在实例化ohe时加参数handle_unknown='ignore' # ohe.handle_unknown='ignore' df2 = pd.DataFrame(df['Embarked'].ffill()) # 填充空缺值, 不然出错 encoded = ohe.fit_transform(df2) encoded = pd.DataFrame(encoded,columns=['Embarked_C', 'Embarked_Q', 'Embarked_S']) df_plus = df.join(encoded) # df_plus.drop('Embarked', axis=1) # print(encoded)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(未完待续)
# 1.5 新增特征
# 2. 数据描述
- 连续变量
- 描述统计量: 平均值,中位数,众数,最小值,最大值,四分位数,标准差等
- 图表:分箱频数分布表, 直方图, 箱线图
- 离散变量
- 描述统计量: 特征分布(频数), 占比
- 图表: 频数分布表, 柱状图, 饼图
# 3. 考察关系
- 连续变量:
- 散点图
- 热力图
- 离散变量:
- 交叉分组表
- 堆积柱形图
探索性数据是一种态度,是对我们相信存在抑或不存在的事物保持灵活的审视
John Tukey